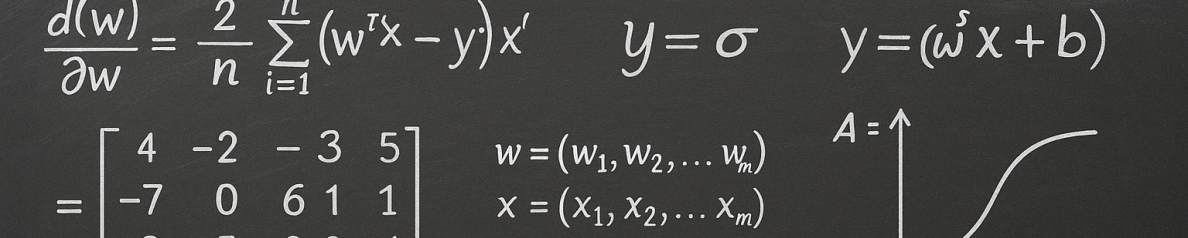Controlling Generalization in Quantum Machine Learning via Fisher Information Geometry and Dimensionality Reduction

We derive geometry‑aware generalization bounds for quantum ML, showing how Fisher information and dimensionality reduction tighten performance guarantees.

We combine quantum Fisher information geometry with covering-number analysis to obtain explicit high‑probability generalization bounds for quantum machine‑learning models, and we explain how reducing the effective dimensionality of the parameter space leads to tighter guarantees.

TL;DR

We bound the generalization error of quantum ML models using the quantum Fisher information matrix.
The bound tightens as the effective dimension 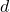 $d$ drops, giving a 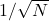$1/\sqrt{N}$ improvement with more data.
Our approach links geometry, covering numbers, and dimensionality reduction: tools rarely combined in quantum learning theory.

Why it matters

Quantum machine learning promises speed‑ups for tasks such as chemistry simulation and combinatorial optimization. However, a model that works well on a training set may fail on new data, a problem known as over‑fitting. Classical learning theory offers tools like Rademacher complexity and covering numbers to predict over‑fitting, but quantum models have a very different parameter landscape. By translating those classical tools into the quantum domain, using the quantum Fisher information matrix (Q‑FIM) to describe curvature, we obtain the first rigorous, geometry‑aware guarantees that a quantum model will perform well on unseen inputs. This helps practitioners design models that are both powerful and reliable.

How it works (plain words)

Our method proceeds in four intuitive steps:

Characterise the landscape. We compute the quantum Fisher information matrix for the model parameters. The determinant of this matrix tells us how “flat” or “curved” the parameter space is.
Control complexity with covering numbers. Using the curvature information, we bound the number of small balls needed to cover the whole parameter space. Fewer balls mean a simpler hypothesis class.
Translate to Rademacher complexity. Covering‑number bounds feed into a standard inequality that limits the Rademacher complexity, a measure of how well the model can fit random noise.
Derive a high‑probability generalization bound. Combining the Rademacher bound with a concentration inequality (Talagrand’s bound) gives an explicit formula that relates training error, sample size 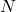$N$ , effective dimension 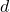$d$ , and geometric constants.

Finally, we note that many quantum circuits can be projected onto a lower‑dimensional subspace (e.g., by pruning or principal‑component analysis). Reducing $d$ shrinks the exponential term in the bound, directly improving the guarantee.

What we found

Our theoretical analysis yields a clear, data‑dependent guarantee:

The generalization error decays as 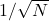$1/\sqrt{N}$ , with a prefactor that depends on the effective dimension 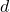$d$ and a geometry term $C'$ .
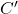When the Q‑FIM has a positive lower bound on its determinant (i.e., the parameter space is well‑conditioned), the exponential factor 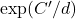$\exp(C'/d)$ remains modest.
Dimensionality reduction, whether by explicit pruning, low‑rank approximations, or post‑training projection, reduces 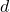$d$ , which tightens the bound and makes the model less prone to over‑fitting.

Key equation

$R(\theta) \le \hat{R}_N(\theta) + \frac{12\sqrt{\pi d}\,\exp\!\bigl(C'/d\bigr)}{\sqrt{N}} + 3\sqrt{\frac{\log(2/\delta)}{2N}}\,,$

This inequality states that the true risk $R(\theta)$ is bounded by the empirical risk $\hat{R}_N(\theta)$ plus two correction terms: a geometry‑dependent term that shrinks with $\sqrt{N}$ and a confidence term that scales with $\sqrt{\log(1/\delta)/N}$ .

Here $C' = \log V_\Theta - \log V_d - \log m + d\log L_f^p$ , where $V_\Theta$ is the volume of the full parameter space, $V_d$ the volume of a $d$ ‑dimensional subspace, $m$ a lower bound on $\sqrt{\det(F(\theta))}$ , and $L_f^p$ a Lipschitz constant for the noisy model $f_{\theta,p}$ .

Limits and next steps

Our analysis relies on three assumptions that are common in learning‑theory work but may limit immediate practical use:

We assume the loss function is Lipschitz continuous and the gradients of the quantum model are uniformly bounded.
We require a positive lower bound 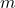$m$ on the determinant of the Q‑FIM; highly ill‑conditioned circuits could violate this condition.
The exponential term 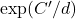$\exp(C'/d)$ can become large if the parameter‑space volume or Lipschitz constant is not carefully controlled.

Future research directions include:

Designing training regularizers that directly enforce a well‑behaved Q‑FIM.
Developing quantum‑specific dimensionality‑reduction algorithms that preserve expressive power while lowering $d$ .
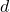Empirically testing the bound on near‑term quantum hardware to validate the theoretical predictions.

FAQ

What is the quantum Fisher information matrix (Q‑FIM) and why does it matter?: The Q‑FIM measures how sensitively a quantum state (or circuit output) changes with respect to small parameter variations. Its determinant captures the curvature of the parameter landscape; a larger determinant indicates a well‑conditioned space where learning is stable, which directly reduces the complexity term in our bound.
How does reducing the effective dimension 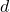$d$ improve generalization?: All three terms in the bound become smaller when 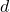$d$ drops. In particular, the factor 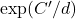$\exp(C'/d)$ shrinks, and the prefactor 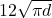$12\sqrt{\pi d}$ scales with 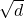$\sqrt{d}$ . Dimensionality reduction therefore tightens the guarantee and makes the model less able to fit random noise.
Is the bound applicable to noisy quantum hardware?: Yes. Our derivation explicitly includes a noise parameter 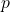$p$ through the model 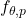$f_{\theta,p}$ and shows that the bound remains valid as long as 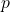$p$ stays within a regime where the Lipschitz constant 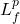$L_f^p$ and the Q‑FIM lower bound 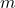$m$ are preserved.

Read the paper